技术帖｜悬索桥的跨越能力为何如此强？

专家见解
　　悬索桥的上部主体结构主要承受拉力，这几乎是效率最高的结构体系。  

8 e* V& B- R/ ~

" G7 H' J5 [3 D5 v2 e

　　由中铁大桥局承建的连镇铁路镇江长江大桥（效果图）是我国首座公铁两用悬索桥，主跨1092米，荷载及运营速度均属世界第一。
　　大桥设计师、中国工程设计大师徐恭义曾在接受记者采访时表示，镇江五峰山长江大桥，悬索桥主跨为1092 米，钢桁架加劲梁双层桥面结构，上层为8 车道高速公路，下部为4线高速铁路。根据河道条件，该项目位于长江下游镇扬河段的大港水道。大桥地处江苏省内河道最狭窄的地方，大港水道和畅洲汊道汇流点至五峰山，长约8.3公里，水道微弯，向南凹进，断面形态呈“V”字形，江面宽仅约1.2公里，平均过水断面积为29954平方米。河面的狭窄，致使这里水域船运繁忙，如果选用其他桥型就会占用河道面积，使这里的河面更加拥堵，造成不便。根据实际情况，需采用1000米左右的跨度修建桥梁。针对此跨度要求，设计过程对斜拉桥和悬索桥两种具备跨越能力的桥梁结构形式进行了同等深度的比较。结合地形条件，单跨悬索桥更具技术经济优势。经过评审，一致推荐采用悬索桥结构。
8 S5 |# t+ @6 g$ ^- }: G, Z        五峰山长江大桥在设计之初，就充分运用了已开通运营的特大跨度桥梁的实测数据和计算方法，对中国的高速重载铁路荷载进行了仔细的分析研究，确保悬索桥结构具有足够的受力安全以及行车舒适性。

) @: h" F% j2 a7 V6 A# o" @
　　简单说，拿筷子做类比。随便一用力就可以把筷子掰断，这就是筷子在受弯；但几乎很少有人能够把筷子拉断，这就是筷子在受拉。几乎所有的材料，受拉的效能都要远远高于受弯的效能。
1 I/ H8 n7 `' [
　　想一下晾衣服。受弯的例子就是晾衣杆（木头、竹子、金属），这些杆子都要有足够的直径，否则很容易就被衣服压断了。受拉的例子则是晾衣绳，很细的一根绳子，所用的材料比木杆子少得多，晾上衣服之后下垂的弧度很大，但一般情况下很难被拉断。

0 n0 C2 f* n9 q0 Y, H# i2 T5 j0 Y

3 G, ]( [+ L; @& I  M) n

9 X( N  S6 M' L8 G　　与受拉相比，受弯是一个效率极低的承载方式。一定程度上，提高结构效能就是尽量的把受弯转化为受拉或者受压。如果同时能够做到尽量减轻结构自重，那就更完美了。拱结构就是转化为受压的例子，而悬索桥则是转化为受拉的例子。
. A4 V' Y( d! X

$ [0 Z( M0 A: w2 D

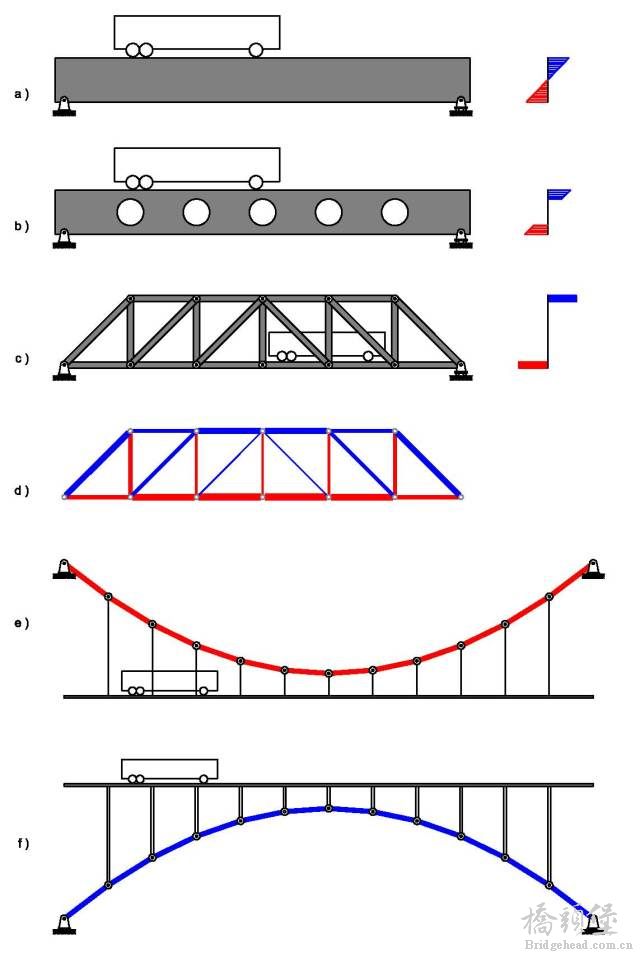
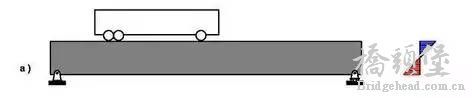
　　a 图就是最普通的梁式桥，完全依靠受弯承载。这种形式非常常见，地铁、高架、小型公路桥梁，几乎全部是这样的。右边是它的截面的应力分布，上下边缘受力大，中间位置几乎为零。也就是说，整个截面的应力并不是平均分配的，尽管中间位置几乎没有应力，但是，只要上下边缘达到了极限，整个截面同样可以被破坏。
, c) b1 Y( m9 L- ^1 G6 T- K$ f

  m( w) G3 Q5 T0 ]　　福建泉州万安桥
8 C/ t/ }5 O6 U+ n. i$ Z
　
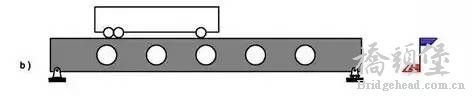
" S! }! X9 ]) s9 |8 n; B   　既然中间截面几乎为零，那么为什么不把它们省略呢？于是，就有了 b 图这种开孔梁。截面中间部位应力很小的那些地方被省去，减轻了自重。拉压应力集中在上下边缘处。
6 ^( e3 i; ?' K

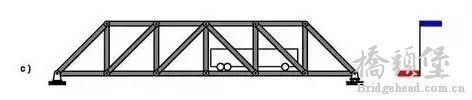
& P( f3 Q: L/ M+ S7 a; g+ F3 m　　把这个趋势进一步扩大，也就是把原来的梁式结构进一步格构化，去掉应力小的部位，保留最基本的部位，我们就得到了 c 图的这种桁架结构。

9 D0 b" q1 a/ C5 K( s6 w* h3 i
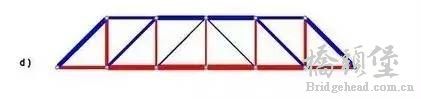
　　d 图是它的大致内力分布，红色受拉，蓝色受压。它的截面分布更加合理，上弦杆件受压，下弦杆件受拉，中间没用的部位全是空的。著名的南京长江大桥就是这样的结构型式。
& j1 J6 [9 P8 }$ }: X; g! z/ T8 L

　　南京长江大桥
4 l( `  c% ]" @0 f. [
2 v5 [# Y5 R2 u" l# m
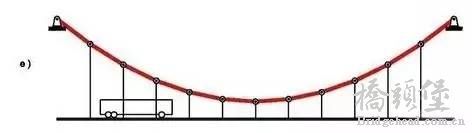
9 q% a" N: j1 Z" t* T- K　　如果把这个最优化的趋势做到极致，那就达到了 e 图这种的悬索结构。整个悬索承受同样大小的拉力，整个悬索的拉力由支座处的锚固平衡。其实这种结构非常好理解，把 e 图想象成一根晾衣绳，上面晾了11件衣服，而晾衣绳的两端，需要牢固的栓在墙上或者柱子上。很容易理解吧？比较难理解的是如何解决锚固处巨大的力？
  d) S2 l" z+ Z; {
" y8 x- F, O$ a" n: L
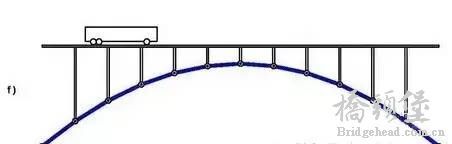
　　f 图所示的拱桥就是另一个方向的极致，与 e 图上下对称，f 图中的拱结构只承受压力，也不承受弯矩。但与纯受拉的悬索结构相比，受压的拱结构还牵扯到稳定问题。举个例子，你用脚踩放在地上的空易拉罐，很难把它踩碎，但是很容易就把它踩变形、踩扁了。因此，拱结构的效率还是比不上悬索结构。



: {  K% t7 R+ J) v. P& `1 F
. W1 [# Y* |; g* B% A) E1 X9 Q

　　那为什么悬索非得是这种形状呢？也很好理解，弄一根铁链，或者自行车链条，两端固定，中间自由下垂，得到的就是上面 e 图的这个形状。自由绳索在自重作用下自由下垂所形成的曲线，一般称为悬链线。观察一下蜘蛛网，它们就是近似的悬链线。

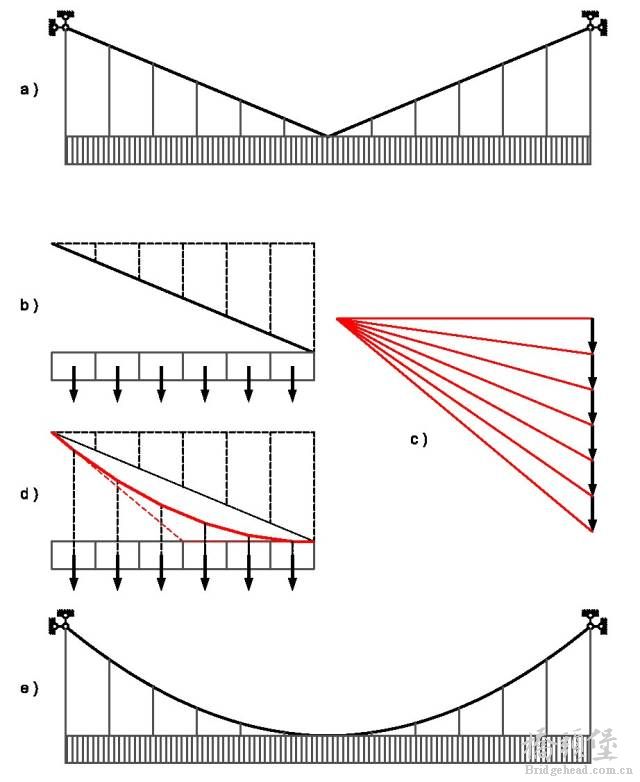
假设承受均布荷载的悬索，最初始的形状是 a 图这种倒三角形。因为是对称结构，所以取它的一半进行分析。如 b 图所示，类似微积分的概念，近似把这一半均匀分为6份，每份荷载相同。c 图是这种情况下的力多边形，而 d 图中的红色折线就是这一组力的索多边形。以这条红色折线为几何构形，我们得到 e 图所示的悬索。因为考虑的是均布荷载，所以不需要再二次迭代了，再迭代一次的结果只会是同样的这条红色折线。因此，红色折线就是均布荷载下的最优悬索，不承受弯矩，只承受拉力。注意，这个不是悬链线，而是一条抛物线，因为它承受的是均布荷载，而不是自重。

关于悬链线的数学认知，说起来也很有代表性，人类对于知识的认知就是这样的渐进式的过程。亚里士多德认为抛出物体的运动轨迹是先直线，然后再下落。伽利略意识到亚里士多德错了，得出了正确的抛物线的表达式，但是，伽利略错误的认为一条悬链自然下垂，得到的也是一条抛物线。随后，容吉乌斯指出，在受水平向均布荷载的情况下，悬链的形状才是抛物线，也就是我们上面 e 图的情况。由于悬链的自重是沿曲线方向分布的，水平方向的荷载分量并不均布，所以自然悬链不是抛物线。虽然容吉乌斯指出了伽利略的错误，但他没能找到正确的答案。直到1691年的一次数学竞赛中，莱布尼茨、惠更斯和约翰·伯努利才各自独立得出了正确的悬链线的数学表达形式。

- T) I6 p; y  s! n9 S

当然，制约悬索桥跨度和安全性能的不仅仅是竖向荷载，还有侧向的抗风设计。1940年，美国塔克马海峡大桥在风中坍塌，引起了工程学界对抗风设计的重视。今天的悬索桥，技术水平已经达到了很高的程度。目前最长跨度的悬索桥是日本的明石海峡大桥，主跨1991米。其原设计为1990米，但1995年的阪神大地震震中距大桥只有4公里，导致正在建设中的两侧桥塔之间的水平距离增加了1米。

: f$ ~1 Q  Y1 y! o2 g" N& u- `

从悬索的数学推导，到惊人的主跨接近2000米的大桥，这就是一条从简单理论模型到复杂实际设计的道路。数学理论和力学理论如何指导实际的工程设计，这就是一个很好的例子。而所谓工程师，就是能够优雅简洁的完成这一过程的人。

                    

图文并茂深入浅出啊，多谢楼主分享啦~~~

受教了 生动形象 很容易理解

绝对好贴。赞！！！！！！

理论功底扎实，分析深入浅出啊

受教了。比一些大学授课教师讲的要好多了

非常好的一篇文章。。赞。。

非常好！很到位！

讲的真好，下载了，谢谢

讲的很好，深入浅出，形象生动。